Consider a closed composite system consisting of two simple systems separated by a barrier that is impermeable to entities and pressure, but which allows the flow of relation heat.  (The physical interpretation here would be two organizations isolated except for the flow of memes, i.e.  information.  A recent major example would be the relation between the former Soviet Union and the West.) N_k and V are constant for each subsystem, but the energies of each subsystem are allowed to change subject to the conservation restriction

            E⁽¹⁾ + E⁽²⁾ = constant

imposed by the closure of the system as a whole.  By the fundamental postulate at equilibrium the values of E⁽¹⁾ and E⁽²⁾ are such as to maximize the entropy.

The condition for the extremum is

            dS = 0.

The additivity of entropy gives

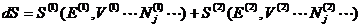
Since only E is allowed to change,

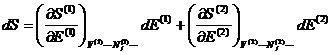
Using the definition of temperature, this becomes

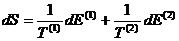
By the conservation condition

giving

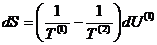
The equilibrium condition demands that dS vanish for arbitrary values of dU⁽¹⁾, therefore

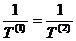
I have introduced the quantities of heat flux and temperature without giving an interpretation as to what they represent in a system.

In physical systems temperature is a measure of the average kinetic energy of the microscopic components and heat flux is a measure of the transfer of this kinetic energy.  The exact relationship between temperature and microscopic component energies can be very complex.  Examples for ideal gases can be found in Callen [1960, Appendix D, 324-342].

In human systems temperature is a measure of the average rate at which entities change their relations.  The mathematical demonstration of this is exactly parallel to the demonstration of temperature and kinetic energy relationship in physical systems.  I shall not present that demonstration here, however the result is

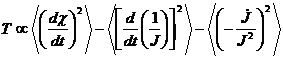                                           (9.4)

I believe it useful to point out this relation to indicate that the concept of relation temperature corresponds to the intuitive conception, that temperature would be proportional to the rate of entity interdependence change.  For example, one might say that a human system with rapidly changing relations is hot.  Or, for example, a human system where the component entities are doing the same thing the same way with the same relationships between entities is cold, even though the entities may be very busy.  Or, for still another example, high temperature systems contain individuals or organization of higher kinetic relation energy and quickly invade lower temperature systems composed of lower kinetic relation energy entities.

One can easily see that this dynamic can be applied to the global expansion of the European enterprise, the East India Trading Company, the geographic spreads of the United States from East to West, and many other historical situations.  It is my intent that the application will be quantitative not just metaphoric.  However, that must wait for a bit more of the theory development and the development of the simulation capability.  The complexity of the situation is not reducible to a set of simple analytic expressions and must therefore be dealt with in computer based simulations.

It is also easy to show [Callen, 1960, 38-40] that heat flows from the higher temperature system to the lower temperature system and that T > 0.  This also corresponds to the intuitive concept of what temperature must mean.

ç  Prior Page of Text     Next Page of Text è
(C) 2005-2014 Wayne M. Angel.  All rights reserved.