Postulate II.  There exists a function (called the entropy S) of the extensive parameters of any composite system, defined for all equilibrium states and having the following property.  The values assumed by the extensive parameters in the absence of an internal constraint are those that maximize the entropy over the manifold of constrained equilibrium states.

                                                                                                Callen [1960, 24]

                        All problems in thermodynamics are essentially equivalent to the basic problem .  .  .  the basic problem can be completely solved with the aid of the extremum principle if the entropy of the system is known as a function of the extensive parameters.  The relation that gives the entropy as a function of the extensive parameters is known as a fundamental relation.  It therefore follows that if the fundamental relation of a particular system is known all conceivable thermodynamic information about the system is ascertainable there from.

                        The importance of the foregoing statement cannot be overemphasized.  The information contained in a fundamental relation is all-inclusive - it is equivalent to all conceivable numerical data, to all charts, and to all imaginable types of description of thermodynamic properties.  If the fundamental relation of a system is known, there remains not a single thermodynamic attribute that is not completely and precisely determined.

            Postulate III.  The entropy of a composite system is additive over constituents subsystems.  The entropy is continuous and differential and is a monotonically increasing function of the energy.

                                                                                                Callen [1960, 25]

Thus    

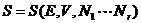                                                        (9.1)

Several consequences follow from these postulates.  These consequences follow because of the mathematical form which I postulate applies not only to physical systems but also to human organizational systems.  Since these consequences are well described in many works, I shall simply state them here.  Callen [1960, 26], for example, gives an explanation of them.

The entropy of a simple system is a homogenous first-order function of the extensive parameters.

Thus if all of the extensive parameters of a system are multiplied by a constant , the entropy is multiplied by the same constant.

       .

  .

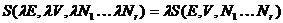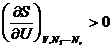Equation (9.1) can be inverted to yield

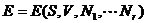                                                        (9.2)

This is an alternative form of the fundamental relation, and it also contains all thermodynamic information about the system.  In this form the entropy maximum principle can be restated as an energy minimum principle.

At this point an obvious question to ask is, "What is entropy? Interestingly, the theory of thermodynamics can precede without answering this question.  Since it is not necessary and because it is well known and demonstrated in many texts, I will not take the time to demonstrate but only state the answer.

            The entropy of any macrostate is proportional to the logarithm of the number of microstates associated with that macrostate.

                                                                                                Callen [1960, 318]

ç  Prior Page of Text     Next Page of Text è
(C) 2005-2014 Wayne M. Angel.  All rights reserved.